年前,Mamba被顶会ICLR拒稿的消息曾引起轩然大波。
甚至有研究人员表示:如果这种工作都被拒了,那我们这些「小丑」要怎么办?

这次,新一代的Mamba-2卷土重来、再战顶会,顺利拿下了ICML 2024!

仍是前作的两位大佬(换了个顺序),仍是熟悉的配方:

论文地址:https://arxiv.org/pdf/2405.21060
开源代码和模型权重:https://github.com/state-spaces/mamba
不同的是,作者在更高的视角上,统一了状态空间模型(SSM)和注意力机制(Attention),也就是文章标题所说的「Transformers are SSMs」。
——这下咱们都是一家人了,不用动不动就「打生打死」了。

性能方面,Mamba-2采用了新的算法(SSD),比前代提速2-8倍,对比FlashAttention-2也不遑多让,在序列长度为2K时持平,之后便一路遥遥领先。

在Pile上使用300B token训练出的Mamba-2-2.7B,性能优于在同一数据集上训练的Mamba-2.8B、Pythia-2.8B,甚至是更大的Pythia-6.9B。

从理论上整合了SSM和Transformer,同等性能下,模型更小,消耗更低,速度更快。
更重要的是,能够利用GPU的硬件资源(矩阵乘法单元),以及针对Transformer的一系列优化。
——Mamba-2大有一统江湖之势。

1代Mamba,爆发式占领AI社区
事实上,关于1代Mamba的各种研究一直在爆发性地增长,arxiv已经被各种Mamba所占领,谷歌学术的引用量也达到了350多。
后续工作如雨后春笋一般冒出,包括视觉、基因组学、图表等的直接应用,以及回忆能力、上下文学习能力、形式语言表达能力等方面的研究。
作者兴奋地表示:「我们多年来一直在追求的高效序列模型研究路线,真正引起了机器学习社区的共鸣。」
唯一遗憾的是,Mamba遭到ICLR拒稿,所以关于Mamba到底有没有前途这个事也就被打上了问号。
现在,问题解决了,不但论文被接收了,而且还证明了Transformer和Mamba其实是一家人——
「你说我不行?那Transformer到底行不行?」
值得注意的是,之前很火的Vision Mamba以及另一篇关于Mamba的研究也杀入了ICML 2024。
对于改进Mamba的初衷,作者表示,当前AI社区的大家都在努力解决Transformer的问题,尽管SSM的特性和效果都相当好,但却跟社区的努力方向不一致。
这次的Mamba-2可以把针对Transformer的优化都用上,不浪费大家的努力。

新架构一统江湖
在介绍新架构之前,小编先帮大家简单理一下背景。
状态空间模型SSM之所以如此令人着迷,是因为它们显得如此之「基础」。
比如,它们与序列模型的许多主要范式,都有着丰富的联系。
它们似乎抓住了连续、卷积和循环序列模型的本质,把所有这些元素都包含在了一个简单优雅的模型里。
不过,另一个主要的序列模型范式——注意力机制的变体,却更加无所不在。
然而SSM却总感觉和Attention是脱节的。
在这里,研究者们发出了「灵魂拷问」——SSM和注意力之间的概念联系是什么?有无可能将二者结合起来?
那就要从公式说起了。
状态空间模型SSM可以这么定义:

这是个微分方程,利用导数定义进行代换:

可以得到SSM的解:

这个东西就跟RNN一毛一样了:

所以可以认为SSM等价于RNN。
如果将RNN的递归结构展开,那么它又可以等价于卷积:


此时,便可以利用卷积的特性进行并行训练,而进行推理时又可以享受RNN带来的O(1)复杂度。
当然,好事不能让你全占了,这种结构仍然逃不过固有的梯度爆炸(或消失),以及难以胜任选择性复制和上下文学习等任务。

为此,Mamba在SSM的基础上加入了能够随输入变化的参数。

不过这样做的代价是失去了固定kernel带来的并行性,所以作者另辟蹊径,使用前缀和的方式来加速RNN的训练。

不过,从计算角度来看,Mamba在硬件效率上仍然远不如注意力机制。
原因在于,目前常用的GPU、TPU等加速器,是为矩阵乘法进行过专门优化的。

1代Mamba吃不到硬件矩阵运算单元的红利,尽管推理时有速度优势,但训练时问题就大了。
所以作者就想,我能不能把Mamba的计算重构成矩阵乘法呢?
于是,新一代的Mamba诞生了。
结构化状态空间对偶性:SSD
Mamba-2的核心,是结构化状态空间对偶性(State Space Duality,SSD)的概念:
1. SSD模型指的是一个特定的独立层,比如注意力层或状态空间模型(SSM),可以被整合到深度神经网络中;
2. SSD框架是一个用于推理该模型(以及更多理论连接)的通用框架;
3. SSD算法是一种比以前的SSM更高效地计算SSD层的算法。

SSD框架(红色,蓝色):状态空间模型(即半分离矩阵)和结构化掩码注意力涵盖了大量高效的序列模型。它们的交集就是SSD模型(紫色)
原始的Mamba(或更准确地说,其核心「S6」层)实际上是一个具有对角结构的选择性状态空间模型(SSM)。
Mamba-2的SSD层只做了一个小改动:它进一步限制了对角矩阵𝐴,使其成为标量乘以单位矩阵的结构。换句话说,𝐴的对角元素必须都是相同的值。
在这种情况下,𝐴可以表示为形状(𝑇),并且还可以将𝐴𝑡识别为一个标量(有时会表示为𝑎𝑡)。
所谓「对偶性」是指,方程(1)(标量-恒等结构𝐴𝑡的情况)和(3)中定义的两个模型实际上是完全相同的模型。
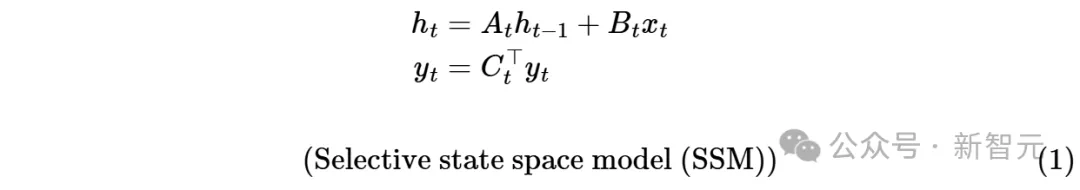
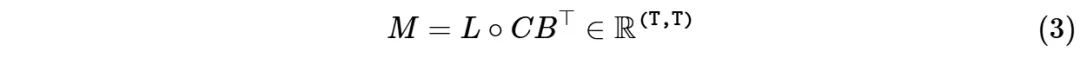
因此,我们可以将其视为一个特定函数:
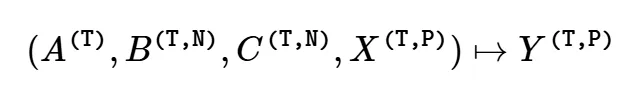
SSD vs. SSM
与之前的状态空间模型(SSM)相比,SSD在递归矩阵𝐴上增加了更多结构:
1. Mamba-1(S6)在矩阵𝐴上使用对角结构,而Mamba-2(SSD)在矩阵𝐴上使用标量乘以单位矩阵的结构;
2. Mamba-1的头维度是𝑃=1(即所有通道完全由独立的SSM控制),而Mamba-2使用的头维度是𝑃>1(默认情况下类似于𝑃=64)。
特别是,这可以通过两种方式视为权重共享:
1. 通过将矩阵𝐴的对角结构限制为标量乘以单位矩阵,递归动态在状态空间的所有𝑁元素之间共享;
2. 这些动态也在给定头的所有𝑃通道之间共享。
换句话说,一个单一的SSM头的总状态大小为𝑃×𝑁,在Mamba-1中由独立的标量递归控制,而在Mamba-2中由单一的共享递归控制。
而这些变化,主要就是为了提高效率——让模型能够以「双重注意形式」查看,从而允许使用矩阵乘法。
因此,与Mamba-1相比,Mamba-2支持更大的状态维度(从N=16提升到了N=64、N=256甚至更高),同时在训练期间速度更快。
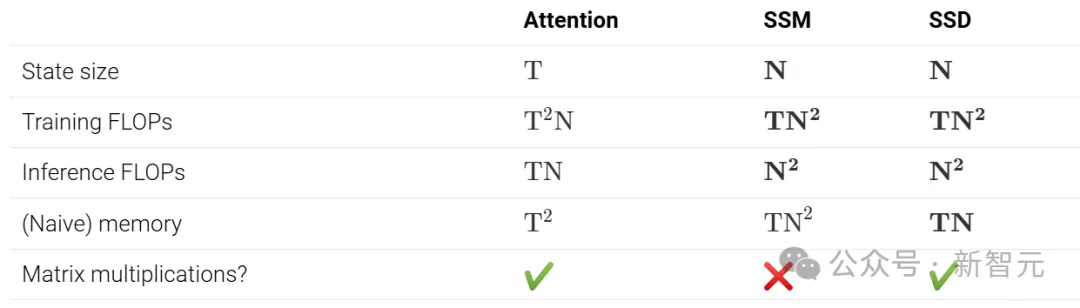
SSD vs. Attention
与标准(自)注意力机制相比,SSD只有两点不同:
1. 取消了softmax归一化;
2. 以乘法方式应用单独的元素级掩码矩阵。
第一个不同之处在于,它将模型的有效状态大小从线性减少到常数,并将效率从二次方提升到了线性。
第二个不同之处是SSD与标准线性注意力的区别。一种理解掩码的方法是将其视为依赖于输入的相对位置编码,由于掩码𝐿的存在,标准的注意力得分𝑄𝑖𝐾𝑗会被一个权重𝑎𝑖:𝑗×=𝑎𝑖⋯𝑎𝑗+1所衰减,这可以理解为基于位置𝑖和𝑗之间距离的「折现细数」(discount factor)。
在注意力形式中,这种依赖输入的位置掩码可以解释为Mamba「选择性」的关键因素!
SSD算法
由于Mamba-1的算法和实现没有使用张量核心,因此只能进行小规模的状态扩展(通常为𝑁=16)。
相比之下,矩阵乘法的FLOPs要比非矩阵乘法快得多(最多快16倍):
– A100 GPU有312 TFLOPS的BF16矩阵乘法性能,但只有19 TFLOPS的FP32算术性能;
– H100有989 TFLOPS的BF16矩阵乘法性能,但只有67 TFLOPS的FP32算术性能。
这次,Mamba-2的一个主要目标,便是利用张量核心来加速SSM。
由于SSD连接了SSM和结构化矩阵,计算SSM或线性注意力的高效算法,可以直接对应于「token混合」或「序列混合」矩阵𝑀的不同分解。
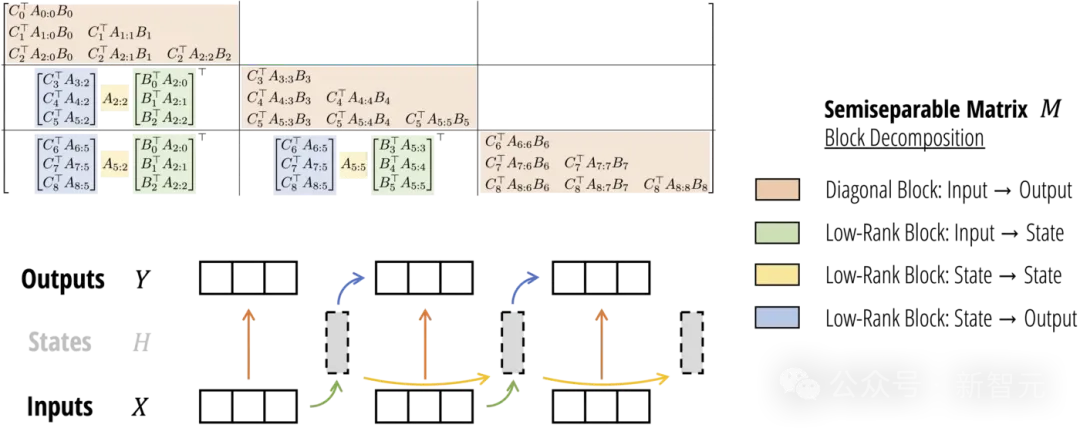
如今,这个算法不仅速度更快,而且比原始的Mamba选择性扫描更容易实现,仅需大约25行代码!
def segsum(x):"""Naive segment sum calculation. exp(segsum(A)) produces a 1-SS matrix,
which is equivalent to a scalar SSM."""
T = x.size(-1)
x_cumsum = torch.cumsum(x, dim=-1)
x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagnotallow=0)
x_segsum = x_segsum.masked_fill(~mask, -torch.inf)return x_segsum
def ssd(X, A, B, C, block_len=64, initial_states=None):"""
Arguments:
X: (batch, length, n_heads, d_head)
A: (batch, length, n_heads)
B: (batch, length, n_heads, d_state)
C: (batch, length, n_heads, d_state)
Return:
Y: (batch, length, n_heads, d_head)
"""assert X.dtype == A.dtype == B.dtype == C.dtype
assert X.shape[1] % block_len == 0# Rearrange into blocks/chunks
X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]
A = rearrange(A, "b c l h -> b h c l")
A_cumsum = torch.cumsum(A, dim=-1)# 1. Compute the output for each intra-chunk (diagonal blocks)
L = torch.exp(segsum(A))
Y_diag = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)# 2. Compute the state for each intra-chunk# (right term of low-rank factorization of off-diagonal blocks; B terms)
decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)# 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries# (middle term of factorization of off-diag blocks; A terms)if initial_states is None:
initial_states = torch.zeros_like(states[:, :1])
states = torch.cat([initial_states, states], dim=1)
decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
states, final_state = new_states[:, :-1], new_states[:, -1]# 4. Compute state -> output conversion per chunk# (left term of low-rank factorization of off-diagonal blocks; C terms)
state_decay_out = torch.exp(A_cumsum)
Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)# Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")return Y, final_state